Quantum Error Correction

Introduction to Quantum Mechanics

Quantum mechanics is the branch of physics dealing with the behaviour of matter and its interactions with energy at atomic and subatomic levels. So, before we get into quantum correction codes, let us go through some fundamental topics of quantum mechanics:

i.Superposition: It is the ability of a quantum system to exist in multiple states till the point at which it is measured or observed. It is often explained with the help of the famous thought experiment "Schrodinger's Cat", which says that until we look inside the closed box that the cat was kept in, we could never be certain if the cat was alive or not.

ii.Entanglement: It is the phenomenon with which the quantum states of two or more particles can be described with respect to each other, even if they lie at vast distances from each other.

What is qubit?

A qubit or quantum bit is analogous to the classical bit in classical computing and can hold a linear combination of 0) and1) (owing to superposition), unlike the classical 0 and 1 bits. A Bloch sphere is used to represent a qubit geometrically.

How does a logical qubit differ from a physical qubit ?

Physical qubits are the physical systems representing the qubits. In contrast, logical qubits are assumed to be perfect and easy to manipulate into any state we desire with higher precision, unlike the physical qubits.

Some logicalgates used in quantum computing :

• Pauli-X: It is analogous to the NOT gate. It flips the bit value, i.e., |0) -> |1) and |1) -> 1 0).
• CNOT or Controlled NOT: It acts on two qubits. The first qubit is the control qubit, and the second qubit is the target qubit. If the control bit is O, then the target bit is unchanged. Else if the control bit is 1, then the target bit is flipped, i.e., |00) -> |00) but |10) -> | 11). Hadamard: This gate is used to create superposition. The input qubit |0) gives the output qubit as |+) = |0) + |1) √2 and |1) as |-) = |0)- |1)√2
• Z Gate: It leaves |0> intact and changes |1> to -|1> and vice versa.
• Toffoli Gate: If three inputs (a, b, c) are passed to this gate, where a and b are the control variables, and c is the target variable, then c is flipped if both a and b are 1

Classical Error v/s Quantum Error :

Since we can classify computers broadly into two types, (i) classical computers and (ii) quantum computers, let's see what kind of errors these computers show!

A classical computer can be anything from a mobile phone or laptop to television, even the smartwatches. So, what exactly might cause an error in these computers?

To begin with the basics of how a computer works, its core principle is that it takes certain inputs, converts them into classical bits (in the form of voltage), works on them through the circuits and chips and gives us an output. This is where something might go wrong, but how?

When we give input to a classical computer, its data is influenced by several things, including temperature, water, bugs, etc. These factors disrupt or manipulate the given input, which gives us an unwanted output. But these errors happen quite rarely; this is due to the fact that information/data travels in a classical computer through wires in a circuit. Each wire contains a thousand electrons which help carry the information along the circuit during calculations and provide an output. So if a few many electrons do get manipulated or destroyed, there's still plenty left to deliver the information correctly.

Let's say we have to send a piece of information called '0'. When '0' is inputted into the computer, all the electrons within its circuits carry the '0' through the circuits for further calculations. If, for some reason, a handful of electrons get destroyed or change their carried information to, let's say, '1', there are still a thousand more electrons delivering the '0', which is the correct information, to the computer.

Is this how a quantum computer works? Yes, but with a few major differences.

To begin with, instead of having a circuit full of electrons to carry information, a quantum computer relies on just one electron known as a qubit to carry the information.

From thousands and thousands of electrons, we are now talking about just one! An electron that is one of the smallest entities in the universe, impossible to see even with an ordinary microscope, let alone our naked eyes, must get influenced by numerous factors like noise, decoherence, etc. This makes passing information through a quantum computer unstable and unreliable. So how do we make sure that the information is not damaged? This is where Quantum Error Correction (QEC) comes into play.

Let's say you have a friend who forgets things quickly. If you want to give him a piece of information that you will later use, it brings uncertainty that they might not remember everything and might give you false information. To eliminate this from happening, you pass the same piece of information to him along with many other friends, although their memory isn't reliable either (lesson - try to make friends with a good memory). But by sharing this information with everyone, you can ask each of them to give the information back to you. This time, instead of just relying on one person's word, you can verify this given information by weighing it against all the other people you shared the same information with.

This briefly explains the logic behind how we rectify an error in a Quantum Computer.

Since we are not allowed to measure the information carried by that one qubit directly, we share that information to a bunch of other qubits in the computers' logic circuit, with an additional code, let's call it Quantum Error-Correcting Code- which uses algorithms to factor in all the qubit's information and processes a valid (correct) outcome. We indirectly ensure that the information we receive/measure at the end is correct.

For instance, if we have to share any information called 'O', we'll distribute this information carried by one qubit to a bunch of other qubits and provide a suitable QEC code to rectify the error after the qubits are influenced by noise or other disturbances, so that at the end when we measure the circuit, the QEC code provides us with the correct information that was sent.

What causes these errors?

Some of the causes like Decoherence and Quantum Noise affect the Quantum states. QEC is a method of protecting quantum information from unwanted environmental interactions like the ones mentioned above.

A quantum computer is defenceless against decoherence and interference. It is vulnerable to some sources like electromagnetic waves and magnetic fields. So, when interference occurs, the quantum state collapses and errors occur. Whereas in the case of a classical computer, atomic and subatomic particles operate the quantum computer. Hence, these actions occur. So typical quantum bits become arbitrary in about one-thousandth of a second, which is difficult to compute.

Let's know about decoherence. It is a process in which the environment interaction occurs. Since perfect isolation can never be achieved, the system is loosely coupled to its environment. That's why the loss of information. And, there might be a possibility of creating entanglement between the system and surroundings. Thus, it affects quantum information, and errors may occur due to heat bath, interaction with other atoms, and interaction with some other fields.

Introduction to quantum error correction:

As mentioned previously, the physical qubits cannot provide precise values of quantum states, leading to errors. Even if the physical qubits improve with time, some amount of error will still remain, mainly due to decoherence. Certain algorithms, which put the physical qubits in an entangling circuit, are deployed for error mitigation to reduce these errors. This helps us create logical qubits from physical qubits called quantum error correction.

Basics of QEC:

Quantum error correction is concerned with identifying and avoiding the noise disturbing the coherence of the qubit. This, in addition to decoherence, also deals with the errors infused by the imperfect gates while encoding or decoding.

How does this error correction process take place?

The process follows 4 major steps: Encoding, Error Detection, Error Recovery, and Decoding. In quantum error correction, the information is encoded, which means the quantum information stored in a single qubit is distributed across multiple supporting qubits. This leads to information protection by consuming a greater number of qubits. The equation is simple: the greater the noise intensity, the greater the number of qubits consumed. Quantum error correction also exercises syndrome measurements to retrieve error information. At the initial stage of quantum error correction, the first code discovered by Shor expressed 9 qubits coping the effect and protecting the information in a single qubit.

Ways of error correction:

1. Bit flip Code:

Bit flip error is the type of quantum error in which the computational state of qubits flips from 0 to 1 or vice versa, and the bit-flip code is used to correct this error. This circuit comprises 3 qubits- 2 ancillary qubits and 1 main qubit. Here, the two ancillary bits are used to correct the main qubit.

This code transfers the computational state of the main qubit to the ancillary qubits using CNOT gates. In case of an error, this state is flipped, and the CNOT gates are again applied to the ancillary bits for correction. Finally, a Toffoli gate is applied to the first qubit to resolve the error.

2. Phase Flip Code : This code is used to correct the phase flip error. So, before we see the phase flip code, let's understand the phase flip error. Phase flip error: This type of error changes the qubit phase by 180 degrees. As you know, this operation is similar to the Z-gate.

fig: Circuit diagram of phase flip code

First, the main qubit (Ѱ or q0) is entangled with two other ancillary qubits(two I0> qubits) using two C-NOT(CX)gates. After that, all the three qubits are passed through Hadamard(H) gates to put them in superposition. Now, when the main qubit encounters a phase flip error, its phase is changed. Also, notice that it is only the main qubit that faces phase flip error and not the ancillary qubits. After this, another Hadamard gate is applied to all the qubits to bring them out of superposition. While the two simultaneous H-gates on the ancillary qubits give the qubits themselves (i.e., return |0>), an H-gate is followed by a Z-gate, and another H-gate acts as a Pauli(X) gate to the main qubit. The last two C-NOT gates and Toffoli gates are used to correct this qubit after the action of the X-gate on it.

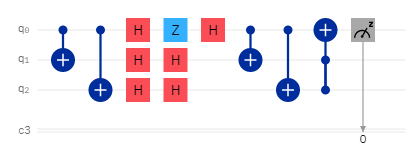fig: A simulation of the phase flip error using Z-gate:

Let's take an example to understand the working of this code. Let q0=0 now after all qubits are passed through H-gate q0=q1=q2= (|0>+|1>)/√2. Now when q0 faces the error, it becomes(|0>-|1>)√2. When H-gates are applied again, the qubits are q0=|1> q1 =|0> q2 =|0>. After the next two CX-gates, q1 and q2 become |1>, and after the Toffoli gate, q0 becomes |0>, solving the error. Similar functioning is seen for other possibilities.

Applications of Quantum Error Correction :

Quantum error correction has added a new layer to the profile of quantum computing, Let's look at some of its applications:

1. Quantum metrology plays a vital role in science and technology. It is used in making highly sensitive measurements of physical parameters using quantum theory to describe physical systems, such as quantum entanglement. But practically, it is vulnerable to errors such as decoherence. This is where quantum error correction plays a role and helps resolve these errors.
2. Quantum computing has efficient algorithms to solve certain issues, such as prime factorization, which are impossible to trace using classical computers. The chances of practical implementation are limited due to decoherence. In this, the external environment causes random errors in the calculation. To combat this problem, quantum error correction schemes are implemented in which a single qubit is encoded as a large number of qubits to resist the errors.
3. Quantum error correction also has an application to quantum sensing with trapped ions. Quantum enhanced sensors try to improve the high precision sensing in the determination of fundamentals of nature, but quantum sensors lose their sensitivity in the presence of noise. To protect them, quantum error correction codes are proposed. Here we introduce a quantum error correction scheme which stabilizes the trapped-ion qubit.

Conclusion :

Quantum Computers are very sensitive devices. A small change in temperature or other external conditions can lead to errors. It is very important to resolve these errors to achieve 'Quantum Supremacy'. Methods such as repetition codes have been developed to detect and resolve these errors. Although these methods solve the errors, they don't have a 100% probability, and the probability of it succeeding is dependent on the probability of the phase flip error occurrence.