Interacting with Atoms who offer QUANTUM MEMORY!

Hello friends. I am an atom.

The building block of everything around you. Allow me to narrate to You my fascinating story!

The birth of my concept was triggered in ancient Indian and Greek philosophy. Indian philosophers called me 'Parmanu', the basic unit of all energy and material entities in the universe, while Greek philosophers called me an 'atom', the smallest possible particle of matter that could not be subdivided.

A better understanding of me began through a series of experiments in the early 19th century, which revealed that I was made of smaller particles, happened to be negatively charged elections, positively charged protons, and no charge neutrons, whereinelectrons are mass-less, protons and neutrons are of equal significant mass. At the core, protons and neutrons clustered together to form the nucleus, whereas the electrons revolved around the nucleus like planets revolved around their source star.

Quantum Ambiguity... Wave-Particle Duality

At minute subatomic scale (i.e., quantum level), subatomic particles would behave strangely by not being localized to a specific position and not having specific momentum (velocity) at a given instant of time. Such a notion would be difficult to perceive, as it is against your human intuition. In fact, for a given macroscopic object around you, you would be able to determine its specific position and momentum accurately

In 1927 Werner Heisenberg gave a mathematical description of the uncertainty existing at the microscopic level using a couple of simple inequalities involving the uncertainties. It occurs while measuring any two complementary variables, such as position & momentum or Energy & Time:

Δx * Δp ≥ h/2,

ΔE * Δt ≥ h/2,

where h is reduced Planck's constant (h = h/2π).

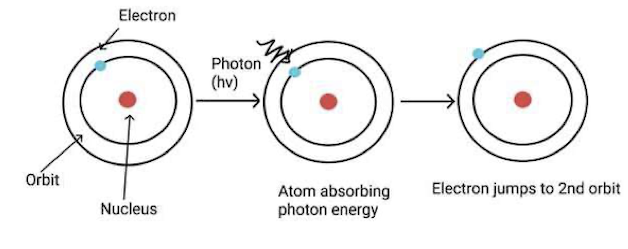
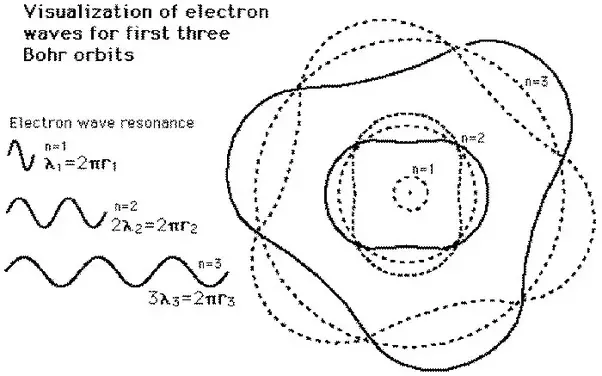
Apart from having uncertainty in my electron's position and momentum, I possess another peculiar property. The electrons revolving around certain fixed orbits do not lose any energy for running around the orbit, which is the main reason for my stability. Otherwise, electrons would collapse to the nucleus by losing energy. Further, everything would have collapsed into the nucleus. Neils Bohr called these orbits stationary orbits having quantized angular momentum _mvr=h, and when external energy is supplied, the electrons jump away from the nucleus into larger orbits.

On the other hand, energy from me is lost only when the electrons jump back to the lowest orbits, wherein the energy difference between the involved orbits is emitted. Max Planck showed that such absorption or emission of energy would always happen in fixed quantized units called 'Photons'. This idea concludes that energy and its flow occur in the form of units of photons, which are also known as pockets of energy. For example, electromagnetic radiation (light) transfers energy as a propagating wave with integral multiples of photons, with each photon having fixed energy (hv).

Planck revealed that photons associated with a propagating wave would also behave like particles, a material property, with duality exhibited by waves. Interestingly, a French physicist by the name of Louis de Broglie suggested that wave-particle duality is not only restricted to radiation; it must be universal and applicable to particles of matter, which must display the wave nature in addition to their conventional material property. He has given a mathematical relation describing the wavelength ƛd associated with the matter waves using a relation of energy to momentum: p=hv/c =h/ƛd, which implies de-Broglie wavelength ƛd=h/p.

When it comes to the duality possible with matter or waves, if you try to probe the atoms, they exhibit only particle nature. The wave nature ceases to exist due to external interaction. Atoms or subatomic particles behaving like waves would substantiate their uncertainty of not being localized, wherein their presence could only be described using Probability. There exists a connection between such probabilities of particle existence to mathematical function describing particle waves called Wave Function, denoted by the Greek letter 'Ѱ'(psi).

Schrődinger Equation... Dynamics of wave Function

Erwin Schrödinger proposed the quantum model of microscopic particles, per se, an atom. wherein electrons are treated as matter waves using the wave function concept. Further, mathematically he connected the wave nature of quantum particles to the state of a quantum system carrying certain energy. The resulting Schrödinger equation became the fundamental equation in Ouantum Physics, analogous to Newton's and law of motion.

F=ma, which connects force acting on an obiect of mass "m" to its acceleration "a" in Classical Physics. There could be multiple possible waves (with the same energy) propagating along the atomic orbit for given election in that orbit.

The wave function Ѱ also carries the information of position or momenta, which could be obtained by taking the square of its absolute value (|Ѱ|2). The information would be in terms of probabilities with which electrons could exist at certain locations or with certain momenta

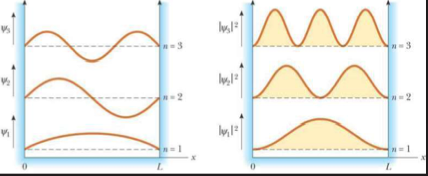
The quantum model of an atom answers many questions that Bohr's and other atomic models failed to do. Quantum particles such as electrons, behaving like waves (spreadvaround in space), substantiate their probabilistic existance at multiple locations.

Finding the probalities of the particle through the wave functions and further running several simulations to reveal the different energy levels would lead you to get a clear understanding of different orbital structures.

Even after all this description, you may think how matter at the quantum level could exist in more than one state. This dilemma could be cleared by Schröndinger's thought experiment involving a cat in a box with some poison container with the possibility of breaking out. If the poison is released due to the triggering of nuclear radiation, then the cat would be dead. Otherwise, the cat would be alive. But the result would be known only when you look into the box. Unless and until you look into the box, vou could not know its state, till then the cat would be in a superposition between dead or alive-the same works with quantum particles. The mere idea that quantum particles could exist in multiple states lead to a path-breaking application in the area of computing knowns as Quantum Memory.

Atoms as Classical Memory & Quantum Memory Devices

In conventional classical computers, the information is stored in the form of Binary Digits, i.e., "Bits" 0 & 1, by permanently aligning the magnetic dipoles of the collection of atoms. This results in the formation of a small bar magnet at a certain memory storing location, wherein the overall alignment would correspond to the bit either 0 or 1 being stored. As mentioned earlier, quantum particles at quantum regimes are bound to possess multiple possible states. For example, an electron in the outermost orbit of an atom. When external energy is supplied by sending in a suitable photon, the electron may excite to a higher energy state or may be confined to the ground State without excitation. Here the electron either being in the ground or excited states could be described in terms of probabilities, which offers a means to simultaneously store two bits of information on the same atom, leading to an elementary quatum bit called Qubit in the area of computing.

If an electron in an atom could be excited with 60% and not be excited with 40%, then the corresponding quantum state that allows storage of Qubit would be a superposition of those two states: Ѱ = 40% not excited + 60% excited. To have consistency with wave function concept, a Physicist by the name of Paul Dirac introduced more handy notations using angle brackets, left angle <| called Bra, and right-angle |> called Ket, and modified the equation as

|Ѱ>= |not excited> + B |excited>

where ɑ and ß being probability amplitudes and |ɑ|² and |ß|² being the corresponding probability densities, respectively with total probability sum to one.

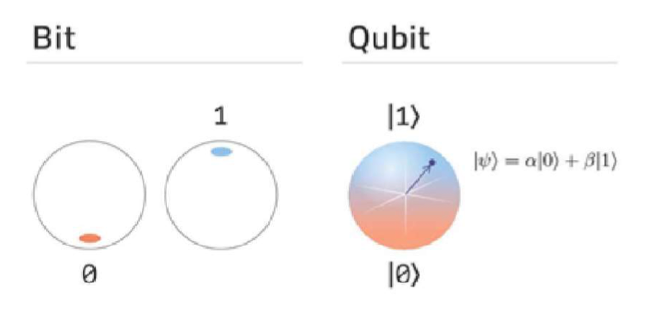
Unlike the classical memory of everyday computers, the states stored in quantum memory would be in a quantum superposition giving much more practical flexibiity in quantum algorithms than classical information storage. There are many other beautiful phenomena in the quantum world, like entanglement, which are rough parches to the human brain. But the nature around you surprises you every time with its behaviour.

                                                                                                 ~Quantum Computing Club
                                                                                                           IIIT Dharward